Matrix Inverse with C++

About Program

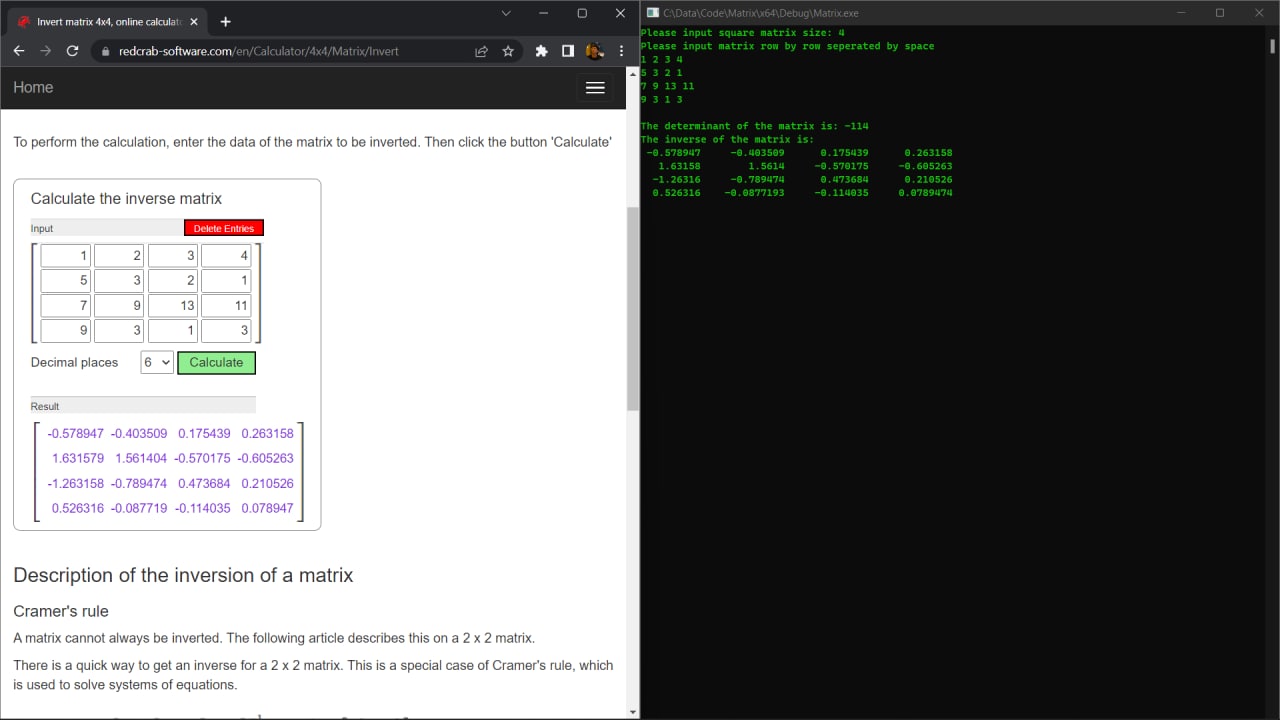
This program can calculate the inverse of square matrices. Users can input the matrix line by line and seperate the columns with space. The method used to calculate the inverse matrix are 1. calculate the determinant of the matrix then 2. take the adjoint of the matrix and 3. divide each element of the adjointed matrix by the determinant.

	/*By Koungmeng 19/9/2022*/
	#include <iostream>
	#include <vector>
	#include <assert.h>
	#include <string>
	#include <sstream>
	//This function can calculate determinant of any square matrix
	float Determinant(std::vector<std::vector<float>>(matrix))
	{
	int rows = matrix.size();
	int cols = matrix[0].size();
	assert(rows == cols); //Raise error is rows != cols
	if (rows == 2)
	{
	return matrix[0][0] * matrix[1][1] - matrix[0][1] * matrix[1][0]; //2x2 Matrix
	}
	else
	if (rows > 2) //For 3x3 matrix and bigger
	{
	int sign = 1;
	float sum = 0;
	for (int i = 0; i < rows; i++)
	{
	std::vector<std::vector<float>>subMatrix(rows - 1, std::vector<float>(rows - 1)); //Create subMatrix in order to calculate minor
	for (int j = 1; j < rows; j++)
	{
	bool b = false;
	for (int k = 0; k < rows; k++)
	{
	if (k == i)
	{
	b = true;
	continue;
	}
	subMatrix[j - 1][k - b] = matrix[j][k];
	}
	}
	sum += sign * matrix[0][i] * Determinant(subMatrix);
	sign *= -1;
	}
	return sum;
	}
	else {
	return matrix[0][0];
	}
	}
	//This is for directly print out the matrix with std::cout
	std::ostream& operator<<(std::ostream& os, const std::vector<std::vector<float>>(&matrix))
	{
	for (int i = 0; i < matrix.size(); i++)
	{
	for (int j = 0; j < matrix.size(); j++)
	{
	std::cout.width(10); std::cout << matrix[i][j] << " ";
	}
	std::cout << std::endl;
	}
	return os;
	}
	//This is for taking user input to construct matrix
	std::vector<std::vector<float>> ProcessMatrixInput()
	{
	int size;
	std::cout << "Please input square matrix size: ";
	std::cin >> size;
	std::vector<std::vector<float>>Matrix(size, std::vector<float>(size));
	std::cout << "Please input matrix row by row seperated by space" << std::endl;
	for (int i = 0; i < size; i++)
	{
	std::string str;
	std::getline(std::cin >> std::ws, str);
	std::istringstream iss(str);
	for (int j = 0; j < size; j++)
	{
	iss >> Matrix[i][j];
	}
	}
	return Matrix;
	}
	std::vector<std::vector<float>> Transpose(std::vector<std::vector<float>>(matrix))
	{
	int size = matrix.size();
	std::vector<std::vector<float>>newMatrix(size, std::vector<float>(size));
	for (int i = 0; i < size; i++)
	{
	for (int j = 0; j < size; j++)
	{
	newMatrix[i][j] = matrix[j][i]; //swap row and col
	}
	}
	return newMatrix;
	}
	std::vector<std::vector<float>> Adjoint(std::vector<std::vector<float>>(matrix))
	{
	int size = matrix.size();
	std::vector<std::vector<float>>newMatrix(size, std::vector<float>(size));
	matrix = Transpose(matrix);
	int sign = 1, signStart = 1;
	for (int i = 0; i < size; i++)
	{
	(i % 2 == 0) ? sign = 1 : sign = -1;
	for (int j = 0; j < size; j++)
	{
	bool r = false;
	std::vector<std::vector<float>>subMatrix(size - 1, std::vector<float>(size - 1));
	for (int k = 0; k < size; k++) //This is for calculating the minor
	{
	bool c = false;
	if (k == i)
	{
	r = true;
	continue;
	}
	for (int l = 0; l < size; l++)
	{
	if (l == j)
	{
	c = true;
	continue;
	}
	subMatrix[k - r][l - c] = matrix[k][l];
	}
	}
	newMatrix[i][j] = sign * Determinant(subMatrix);
	sign *= -1;
	}
	}
	return newMatrix;
	}
	std::vector<std::vector<float>> Inverse(std::vector<std::vector<float>>(matrix))
	{
	float determinant = Determinant(matrix);
	assert(determinant != 0);
	std::vector<std::vector<float>>(adjointMatrix) = Adjoint(matrix);
	for (int i = 0; i < matrix.size(); i++)
	{
	for (int j = 0; j < matrix.size(); j++)
	{
	adjointMatrix[i][j] = adjointMatrix[i][j] / determinant;
	}
	}
	return adjointMatrix;
	}
	int main()
	{
	//std::vector<std::vector<float>>(matrixA) = { {1, -2, 0}, {3,1,5 }, {-1,2,3} };
	std::vector<std::vector<float>>(matrixA) = ProcessMatrixInput();
	//std::cout << Determinant(matrixA) << std::endl;
	std::cout << std::endl;
	std::cout << "The determinant of the matrix is: " << Determinant(matrixA) << std::endl;
	matrixA = Inverse(matrixA);
	std::cout << "The inverse of the matrix is: \n";
	std::cout << matrixA;
	std::cin.get();
	}

view raw meng.cpp hosted with ❤ by GitHub

The output